基于Matlab的雷达信号波形仿真分析
通信工程 201009411 邹江波
指导教师 杨桂芹（副教授）
摘 要： 雷达是集中现代电子科学技术先进成果的一个电子系统，雷达通过对回波信号进行接收检测处理来识别复杂回波中的有用信息。其中，雷达信号波形的选择与设计对雷达系统的工作性能有着非常重要的影响。它直接影响到雷达发射机的选择、信号处理方式、雷达的作用距离与抗干扰、抗截获等很多重要问题。本文首先对雷达系统作简要介绍，接着主要介绍信号的基本变换、常见雷达信号、匹配滤波器、模糊函数，并且基于Matlab平台下，通过实例分析了步进频率信号的距离分辨率、匹配滤波器以及单脉冲信号和线性调频信号的工作性能。
关键字：雷达信号，线性调频信号，步进频率信号，Matlab
1. 雷达简介
1.1 雷达原理及基本组成
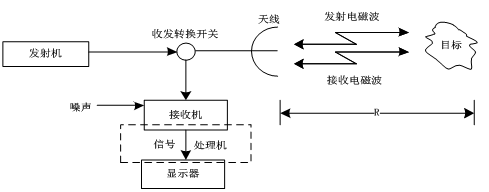
图1.1 雷达工作原理及基本组成
雷达的工作原理如图1.1所示，由雷达发射机产生的电磁能，经收发开关后传输给天线，再由天线将此电磁能定向辐射于大气中。电磁能在大气中以光速（约
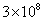m/s）传播，如果目标恰好位于定向天线的波束内，则它将要截取一部分电磁能。目标将被截取的电磁能向各方向散射，其中部分散射的能量朝向雷达接收方向[3]。雷达天线搜集到这部分散射的电磁波后，就经传输线和收发开关馈给接收机。接收机将这微弱信号放大并经信号处理后即可获取所需信息，并将结果送至终端显示。
1.2 常见的雷达信号波形及其作用
表1.1显示了常见的雷达信号波形及其作用，本文主要也是对这三种信号进行仿真分析。
常见雷达信号 |
作用 |
简单脉冲信号 |
早期雷达常用信号 |
线性调频信号 |
用于获得远作用距离和高距离分辨率 |
步进频率信号 |
用于获得高距离分辨率和动态目标测量 |
表1.1 常见雷达信号及其作用
2. 雷达信号波形仿真分析
2.1 信号基本变换
信号的基本变包括傅里叶变换和希尔伯特变换。一个时域信号
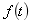的傅里叶变换在数学上可以表示为
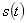的希尔伯特变换可以表示为
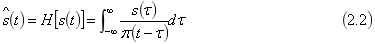
傅里叶变换主要分析信号时宽与带宽的关系。而希尔伯特变换的作用是充当一种理想的移相器，负频率分量相位频移
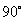，正频率分量相位移动-
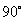。双边频率普信号经过希尔伯特变换后会变成单边正频率谱。
我们知道带通信号频谱通常分布在某个高频附近，在系统设计初级阶段为了分析方便，通常对其等效低通进行分析。因此，通过傅里叶变换和希尔伯特变换，我们可以将带通信号的等效低通表示出来。如图2.2所示，表示出了
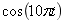的等效低通信号的幅度谱。
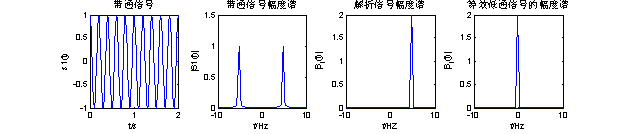
图2.2
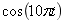的解析信号及其等效基带信号
2.2 线性调频信号
在实际应用中用频率或相位调制信号来获得宽得多的工作带宽，线性调频（LFM）是常采用的方式。在线性调频的情况下，频率在脉宽内线性扫描，频率随着时间的变化增加，我们成为上变频，反之，我们成为下变频。
典型的上变频线性调频信号可以表示为
对线性调频信号进行仿真，分别得到了线性调频信号的实部、虚部以及幅度谱的图像。其中T=10us，B=200MHz截取了部分的图像，如图2.3所示。
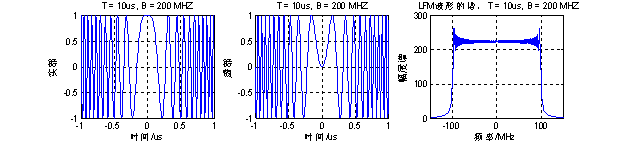
图2.3 线性调频信号仿真图
2.3 步进频率波形
步进频脉冲信号（SFW）包括若干个脉冲，n个窄带脉冲序列以固定的频率步长从一个脉冲到下一个脉冲步进。
下面假设一个SFW信号的步进频率为10MHz，步进数为64。则我们可以计算出SFW信号的距离分辨率和模糊距离窗分比为0.235m和15m。所以当散射体的间隔大于0.235m时，将会在合成距离成像上显示为不同的尖峰。假设距离像起始位置点为
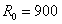m，散射体距离的向量a=[908,910,912]m，形成的图像如图2.4（a）所示。当a=[908,910,910.2]m时，第二个散射体和第三个散射体不能被分辨，形成的图像如图2.4（b）所示。当a=[908,912,923]m时，图像出现混叠，并且第一个散射体和第三个散射体出现模糊现象而不能分辨，如图2.4（c）所示。
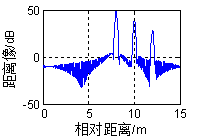
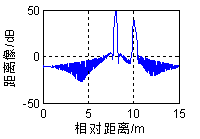
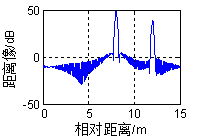
图2.4 SFW信号距离分辨率仿真图
2.4 匹配滤波器
匹配滤波器最独特的功能是当输入端出现信号与加性白噪声时，其在输出端可以产生最大可实现瞬时信噪比（SNR），而且此时的噪声不必是高斯的。通过将雷达接收机传输函数与接收信号相匹配来使得接收机输出端产生峰值瞬时SNR。无论雷达采用何种波形，匹配滤波器输出端的峰值瞬时信号功率除以平均噪声功率等于两倍的输入信号能量除以输入噪声功率的密度，数学表达式如式（2.6）。
下面我们以一个上变频的LFM信号的仿真来说明匹配滤波器的功能。
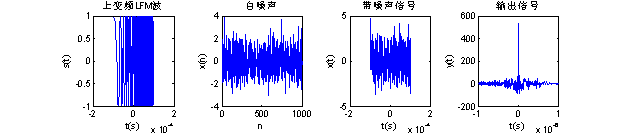
图2.5 匹配滤波器仿真图
从图2.5可以得知，匹配滤波器是在白噪声背景中检测信号的最佳线性滤波器，在叠加高斯白噪声之后的线性调频信号经过匹配滤波，在某个时刻其输出信噪比达到最大。这也就说明，匹配滤波器成功的滤除了白噪声的干扰。
2.5 模糊函数
模糊函数（AF）是分析雷达信号和进行雷达波形设计的重要工具。模糊函数的作用就是当干扰目标与观测目标之间存在着速度和距离差别时，模糊函数定量地表示干扰目标对观测目标的干扰程度。
模糊函数的表达式可以表示为
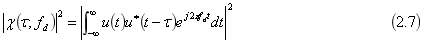
对
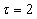s的单脉冲信号和线性调频信号进行仿真分析
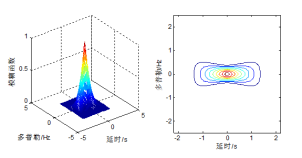
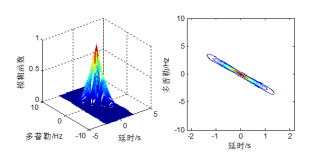
图2.6 单脉冲信号和LFM信号模糊函数仿真图
我们知道解雷达的距离精度由信号的时宽决定，时宽越窄，距离精度越高。而雷达的多普勒频移精度由信号的频宽决定，频宽越窄，多普勒频移精度越高。由图可以知道，单脉冲具有良好的多普勒频移精度，而距离精度较差。LFM信号与单脉冲相比，模糊函数的等高图旋转了一个角度，这就使时间轴的切割交线宽度变窄，使得LFM信号相对于单脉冲距离分辨率提高。同时，频率轴的切割交线宽度变宽，使LFM信号的多普勒频移精度变差。这也就说明，可以通过多普勒频移精度换取距离精度。在实际应用中，根据不同雷达的实际用途可以设置雷达的距离精度和多普勒频移精度。
3. 总结
本文基于Matlab平台下，具体分析了信号的基本变换，常见雷达信号，匹配滤波器和模糊函数。并且通过实例分析了SFW信号的距离分辨率以及单脉冲信号和LFM信号的工作性能。
参考文献
[1] 朱国富，黄晓涛等译. 雷达系统设计MATLAB仿真[M]. 北京: 电子工业出版社，2009
[2] 邢孟道，王彤等译. 雷达信号处理基础[M]. 北京: 电子工业出版社，2008
[3] 丁璐飞，耿富录. 雷达原理[M]. 西安: 西安电子科技大学出版社，2009
[4] 陈伯孝. 现代雷达系统分析与设计[M]. 西安: 西安电子科技大学出版社，2012
[5] 孙亚东. 雷达信号模糊函数理论研究与仿真[D]. 武汉理工大学，2007
Radar Signal Waveform Simulation Analysis Using Matlab
Communication Engineering 201009411 Jiangbo Zou
Tutor Guiqin Yang(Associate Professor)
Radar is focused on the modern advanced science and technology of a electronic system,The radar extracts useful information from the echoes by receiving, inspection and processing. Among them, the selection and design of the radar signal waveform has a very important role, it has a direct impact on the choice of the form of radar transmitters, signal processing, radar range, interference, anti-intercepted so many important issues.This paper briefly introduced the radar system, and then introduces the basic signal transform, common radar signal, matched filter, fuzzy function, and based on the Matlab platform, analysis of the range resolution of step frequency signal, matched filter and work performance of single pulse signal and linear frequency modulation signal by some examples.
甘公网安备62010502000995号 陇ICP备14001560号-2 设计制作 宏点网络
